Let’s first import a few useful libraries:

import numpy as np
import scipy
from scipy.io import loadmat

import matplotlib.pyplot as plt
import matplotlib.cm as cm
from matplotlib.animation import FuncAnimation
%matplotlib inline

from sklearn.model_selection import train_test_split
from IPython.display import HTML

Simulation results are stored in a Matlab file with a .mat format. We’re interested in finding a lower dimensional decomposition of the vorticity defined as \(\boldsymbol \omega = \nabla \times \mathbf u\) where \(\mathbf u\) is the velocity field with two components \(\mathbf u = [u, v]\). Let’s first plot the vorticity

results = loadmat('cyl_flow_data.mat')

m = int(results['m'][0][0])
n = int(results['n'][0][0])
v = results['VALL'][:, 0].reshape((n, m))
u = results['UALL'][:, 0].reshape((n, m))
vort0 = results['VORTALL'][:, 0].reshape((n, m))
tsteps = results['VORTALL'].shape[1]

Use imshow for plotting the vorticity at \(t=0\)

vortmean = np.mean(results['VORTALL'], axis=1).reshape((n, m)).T

plt.imshow(vort0.T - vortmean, cmap=cm.RdBu, interpolation='none')
plt.show()

png

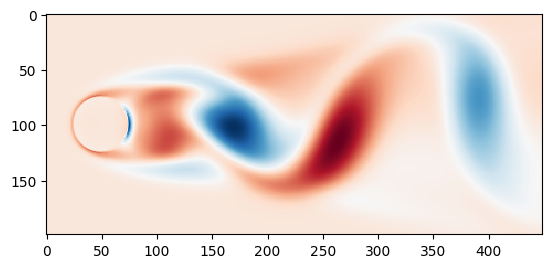
We can also look at the whole simulation by using the matplotlib.animation library

fig = plt.figure()
ax = fig.add_subplot(111)
im = ax.imshow(vort0.T - vortmean, cmap=cm.RdBu)
# vortmean = np.mean(vort, axis=2)
# update the frames based on the parameter i
def animate(i):
    vort = results['VORTALL'][:, i].reshape((n, m)).T - vortmean
    im.set_array(vort)
    return [im]

# run the animation
animation = FuncAnimation(fig, animate, frames=tsteps, interval=20)
plt.close()
HTML(animation.to_jshtml())

New Section

## POD
X = results['VORTALL']

Ynorm = X - np.mean(X, axis=1).reshape(-1, 1)

fig = plt.figure()
r = 0.1 # 100r% of simulation
plt.imshow(Ynorm[:, int(r*Y.shape[1])].reshape((m, n), order='F'), 'jet')
plt.title('Initial Snapshot')
plt.show()


---------------------------------------------------------------------------

NameError                                 Traceback (most recent call last)

/var/folders/q4/_twpfpf54f3f6s17s74p67tc0000gp/T/ipykernel_30195/3291140377.py in <module>
      6 fig = plt.figure()
      7 r = 0.1 # 100r% of simulation
----> 8 plt.imshow(Ynorm[:, int(r*Y.shape[1])].reshape((m, n), order='F'), 'jet')
      9 plt.title('Initial Snapshot')
     10 plt.show()


NameError: name 'Y' is not defined



<Figure size 640x480 with 0 Axes>

U, S, Vt = np.linalg.svd(Ynorm, full_matrices=False)

fig = plt.figure(figsize=(15, 10))

for k in range(9):
    uplot = U[:, k].reshape((m, n), order='F')
    ax = fig.add_subplot(4, 3, k+1)
    ax.imshow(uplot, cmap='jet')
    ax.set_title('mode = %d'%(k+1))
plt.tight_layout()
plt.show()

png

fig = plt.figure(figsize=(15, 10))

for k in range(9):
    uplot = Vt[k, :]
    ax = fig.add_subplot(4, 3, k+1)
    ax.plot(uplot)
    ax.set_title('mode = %d'%(k+1))
plt.tight_layout()
plt.show()

png

POD/SVD is a linear dimensionality reduction technique. Its modes are interpretable as the optimal basis for reconstructing the dynamics/data. However, if the data is nonlinear, POD fails to separate it into orthogonal modes. In that case, a nonlinear dimensionality reduction technique is needed. This motivates the use of autoencoders. Check this paper for examples where Autoencoders are better than PCA: https://people.maths.bris.ac.uk/~maxvd/reduce_dim.pdf

Whether nonlinear dimensionality reduction is required in fluids depends on the problem. Let’s apply it to the flow around a cylinder problem.